Antes de conectar la carga a un transformador sólo existe la intensidad
de vacío io en el
primario que genera la fuerza magnetomotriz necesaria para vencer la
reluctancia del núcleo y generar el flujo en el mismo.
Figura 1:
Transformador excitado en vacío (interruptor S abierto)
En vacío (figura 1), el flujo
canalizado en el núcleo es generado por la fuerza magnetomotriz que produce la
circulación de la corriente de excitación o de vacío.
Un transformador funciona en
carga cuando a su secundario se le conecta una determinada impedancia.
Al conectar la carga (figura 2)
comienza a circular una intensidad i2
en el secundario motivada por la f.e.m.
que se inducía en el secundario. Esta i2
aporta una nueva f.m.m. que tiende a
alterar el flujo en el núcleo.
Figura 2:
Transformador trabajando con carga Z2 (interruptor S cerrado)
Al cerrar el interruptor S comienza a circular una intensidad
por el secundario que producirá una nueva f.m.m.
que se añade a la producida por la corriente de excitación.
Esta nueva f.m.m altera el estado del circuito y tiende a modificar el flujo
circulante.
Sin embargo, como la tensión U1 se mantiene constante
(por ser de la red), el flujo en el núcleo deberá permanecer también constante
para cualquier régimen de carga. Si esto es así, es necesario que aparezca una
nueva componente de corriente en el primario que equilibre la acción
desmagnetizante de la f.m.m.
secundaria (figura 3).
Figura 3: Aparición
de i’2
Como el flujo no puede variar,
pues U1 se mantiene cte,
deberá aparecer una corriente por el primario que compense el efecto
desmagnetizante que provocaba i2.
Esta nueva componente aparece
al conectar una carga y recibe el nombre de componente de carga.
La corriente que circula por el
primario tiene dos componentes:
Una corriente de excitación o
de vacío io, cuya misión es producir el flujo magnético y "vencer"
las pérdidas en el hierro.
Una componente de carga i'2, que equilibra o
contrarresta la acción desmagnetizante de la f.m.m. secundaria para que el
flujo en el núcleo permanezca constante e independiente de la carga.
Circuito equivalente de un Transformador: Modelo de transformador real
(Modelo en T)
Figura 4: Circuito
equivalente de un transformador
Leyenda de la figura 4:
R1: Resistencia de
primario
Resistencia del conductor del
devanado primario.
PFE: Pérdidas por
efecto Joule
Pérdidas por efecto Joule en el
cobre. Son proporcionales al cuadro de la corriente por los devanados (I2R).
Xd1: Inductancia
de primario
Inductancia asociada al flujo
de dispersión en el devanado primario.
Xd2: Inductancia de
secundario
Inductancia asociada al flujo
de dispersión en el devanado secundario.
RFE: Resistencia
Resistencia asociada a las
pérdidas en el hierro por corrientes parásitas.
Pérdidas de Foucault
Las pérdidas por corrientes
parásitas, o de Foucault, son pérdidas por resistencia en el núcleo del transformador.
Son proporcionales al cuadrado del voltaje aplicado al transformador.
Xm: Reactancia
Reactancia asociada a la
reluctancia magnética del núcleo.
Pérdidas por histéresis
Las pérdidas por histéresis
están asociadas con los reacondicionamientos de los dominios magnéticos en el
núcleo durante cada medio ciclo. Son una función compleja, no lineal, del
voltaje aplicado al transformador.
R2: Resistencia de secundario
Resistencia del conductor del
devanado secundario.
Diagrama fasorial del transformador real
Figura 5: Diagrama
fasorial del transformador real
Resistencia y flujo de dispersión en los devanados
Los efectos de la resistencia
de los devanados
La resistencia eléctrica es
inherente al conductor de los devanados. Esta resistencia provoca una cierta
caída de tensión en ambos devanados cuando circula por ellos una intensidad y a
su vez origina un calentamiento por efecto Joule.
Pueden analizarse sus efectos
considerando las resistencias como externas a los devanados (figura 6) y éstos
sin resistencia eléctrica.
Figura 6
La dispersión del flujo
No todo el flujo producido en
los devanados queda canalizado por el núcleo concatenando a los dos devanados.
Una parte del flujo producido en cada devanado no llega a concatenar al otro,
es el flujo de dispersión.
Figura 7: Flujo
mutuo y de dispersión
El flujo mutuo es la parte del
flujo total generado por los devanados y que abraza o concatena a ambos
devanados. Este flujo se canaliza esencialmente en el hierro del núcleo y es
debido al efecto combinado de las corrientes primaria y secundaria.
El flujo de dispersión es la
parte del flujo total generado por cada devanado y que no llega a concatenar
con el otro devanado. Este flujo se distribuye por caminos no magnéticos y en
particular por los conductores y el aire que rodea las bobinas.
Reactancia de dispersión
El flujo disperso introduce una
complicación en la idea de un único flujo por el núcleo del transformador, tal
como se tiene para el transformador ideal. Para poder utilizar esta idea de
flujo común lo que se hace es representar el flujo común por una reactancia
externa al núcleo y éste con un solo flujo común.
Figura 8:
Reactancias de dispersión Xd1 y Xd2 y flujo común φc
La reactancia de dispersión es una
reactancia de núcleo de aire. Este símil es correcto puesto que el flujo de
dispersión hace la mayor parte de su recorrido a través del aire, y tanto su
valor como el de la tensión inducida por él, varían linealmente con la
corriente primaria, tal como ocurre con la inductancia de dispersión.
Pérdidas y rendimiento del transformador
Ver post: Pérdidas y
rendimiento de un transformador
Modelo de transformador referido a su nivel de voltaje primario
Es habitual disponer la red en
paralelo del circuito equivalente al principio del circuito.
Figura 9: Circuito equivalente de un transformador real
con la rama paralelo en el primario
Leyenda de la figura 9:
(1) Resistencia asociada a las
pérdidas en el hierro por corrientes parásitas.
(2) Resistencia de
cortocircuito
Representa la suma de la
resistencia R1 del devanado primario más la resistencia R2*
del devanado secundario referida al primario.
Su nombre proviene de que su
valor se obtiene del ensayo de cortocircuito.
(3) Reactancia de cortocircuito
Representa la suma de la
reactancia Xd1 del devanado primario más la reactancia Xd2* del devanado
secundario referida al primario.
Su nombre proviene de que su
valor se obtiene del ensayo de cortocircuito.
(4) Reactancia asociada a la
reluctancia magnética del núcleo.
Este circuito no tiene en
cuenta la caída de tensión en R1 y Xd1 debida a la
corriente de excitación. Se utiliza preferente cuando son conocidas las
magnitudes U2, I2, cos ϕ2, es decir, las
magnitudes del lado de la carga.
Modelo de transformador referido a su nivel de voltaje secundario
También es común trasladar la
rama en paralelo al final del circuito.
Figura 10: Circuito
equivalente de un transformador real
con la rama
paralelo en el secundario
Leyenda de la figura 10:
(1) Resistencia de
cortocircuito
Representa la suma de la
resistencia R1* del devanado primario referida al secundario más la
resistencia R2 del devanado secundario.
Su nombre proviene de que su
valor se obtiene del ensayo de cortocircuito.
(2) Reactancia de cortocircuito
Representa la suma de la
reactancia Xd1* del devanado primario referida al secundario más la
reactancia Xd2 del devanado secundario.
(3) Resistencia asociada a las pérdidas
en el hierro por corrientes parásitas referida al secundario.
(4) Reactancia asociada a la
reluctancia magnética del núcleo referida al secundario.
Su nombre proviene de que su
valor se obtiene del ensayo de cortocircuito.
En este caso se sobredimensiona
la caída de tensión pues se incorpora unas caídas en R2* y Xd2*
debida a la corriente de excitación. Este circuito es útil cuando se
conocen las características del primario U1, I1, cos ϕ1.
Circuito equivalente aproximado
En la práctica es habitual
despreciar el pequeño valor de la corriente de excitación y no considerar la
rama en paralelo.
Figura 11: Circuito
equivalente aproximado
Leyenda de la figura 11:
(1) Resistencia de
cortocircuito
Representa la suma de la
resistencia R1 del devanado primario más la resistencia R2*
del devanado secundario referida al primario.
Su nombre proviene de que su
valor se obtiene del ensayo de cortocircuito.
(2) Reactancia de cortocircuito
Representa la suma de la reactancia
Xd1 del devanado primario más la reactancia Xd2* del
devanado secundario referida al primario.
Su nombre proviene de que su
valor se obtiene del ensayo de cortocircuito.
Para saber más:
Diagrama fasorial del esquema aproximado (Triángulo de Kapp)
Si se representan en el plano
de Gauss las magnitudes que intervienen en el circuito equivalente aproximado
de un transformador, los vectores Xcc, Rcc y Zcc forman el llamado triángulo de
Kapp.
Figura 12
También puede expresarse el
diagrama en forma porcentual. Todas las magnitudes se dividen por el valor de
U1 y se multiplican por 100.
El ensayo de cortocircuito
Permite obtener los valores
asociados con la rama en serie (pérdidas en el cobre, tensiones de
cortocircuito y parámetros Rcc y Xcc).
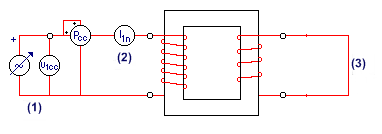
Figura 14: Ensayo
del transformador en cortocircuito
Leyenda de la figura 14
(1) Con una fuente de alimentación alterna se
alimenta el circuito hasta que circule la corriente nominal por el primario.
(2) Con un amperímetro se mide la intensidad que
circula por el primario. Las condiciones de ensayo deben ser tales que la
corriente que circule por este devanado sea la nominal.
(3) El devanado secundario se mantiene abierto.
Para más detalles ver post: “Medida de la tensión de
cortocircuito y pérdidas en carga en Transformadores secos”
http://imseingenieria.blogspot.com/2016/02/medida-de-la-tension-de-cortocircuito-y.html
Post relacionado:
Estudio del funcionamiento del Transformador en
vacío