Experimentalmente se demuestra que las pérdidas en el hierro son aproximadamente proporcionales al cuadrado de la inducción; es decir que, desde el punto de vista del usuario, son preferibles las inducciones bajas. Pero el interés de los constructores de transformadores es dar un valor tan elevado como se pueda a la inducción, ya que, como se sabe, la fuerza electromotriz inducida vale:
y siendo constante, para un transformador dado, los valores de f y de n.
y que, a su vez
obtenemos:
Es decir, que para obtener una fuerza electromotriz dada, cuanto mayor sea la inducción, menor será la sección del hierro y, también, menos cobre se necesitara en los arrollamientos, ya que las espiras de éstos tendrán menos perímetro, como resultado, el transformador será menos voluminoso y más económico cuanto más elevada sea la inducción. Por consiguiente, en lo que a pérdidas en el hierro se refiere, debe solucionarse el problema de forma que no resulte lesivo ni para el constructor ni para el usuario. Para transformadores de distribución las normas internacionales imponen pérdidas máximas según potencias.
Por otro lado, el cálculo de las corrientes de cortocircuito es de interés tanto para el proyectista de transformadores como para el instalador. En efecto, uno y otro han de prever tanto los efectos térmicos como los dinámicos que aquellas corrientes puedan ocasionar, y dimensionar las máquinas, instalaciones y protecciones adecuadamente, de cualquier forma deberemos evitar que aparezcan valores térmicos y dinámicos elevados en le red, teniendo presente que estos efectos crecen según el cuadrado de la intensidad, se comprenderá que este interés será tanto mayor cuanto mayores sean las potencias puestas en juego.
Ejemplo:
Sea el transformador de la figura y su esquema equivalente en el que se produce un accidente de cortocircuito. Distinguiendo entre ensayo de cortocircuito y accidente de cortocircuito por:
Se designa por Icc la corriente de cortocircuito que se desea conocer. Para Xcc constante. Se tiene que:
Ucc suele darse en %, referida a la tensión nominal
resulta:
La corriente calculada es la de cortocircuito en el primario Icc = Icc1. Si se desea la del secundario:
Ejemplo:
En un transformador de 20 000 KVA, 30 000/6 000 V, Ԑcc = 5%
El mismo transformador pero con Ԑcc = 10%, tendríamos:
En este ejemplo podemos observar las elevadas intensidades permanentes de cortocircuito que pueden producirse y como aumentando el valor de Ԑcc (10%), puede lograrse disminuirlas considerablemente. Por esta razón, es por lo que, en los transformadores de gran potencia, suelen emplearse valores de Ԑcc más elevados que en los pequeños.
Transformadores de distribución (50 a 2500 KVA.) Ԑcc = 3 a 6 %.
Transformadores de gran potencia (5000 a 50 000 KVA.) Ԑcc = 7 a 13 %.
Según lo expuesto hasta aquí, podría pensarse que, en cualquier caso, son preferibles valores elevados de Ԑcc. Debemos tener presente el aspecto de las caídas de tensión, con el fin de que estas sean reducidas interesan valores pequeños de Ԑcc. Por tanto, la asignación de la Ԑcc a un determinado transformador es el resultado del compromiso entre los dos aspectos indicados.
La caída de tensión en la generalidad de los casos prácticos es positiva y puede ser nula para un valor ϕ0 del ángulo ϕ más allá de la cual incluso podría llegar a ser negativa.
Esta viene dada por la formula:
en la cual la tensión de cortocircuito Ucc generalmente viene impuesta.
Ejemplo:
Un transformador de 10 MVA 63/20 kV. tiene una tensión de cortocircuito Ucc = 10% y perdidas debidas a la carga igual a 70 kW, la caída de tensión bajo un cos. ϕ = 1 y cos ϕ = 0,8 serian:
En otras ocasiones la tensión de cortocircuito de un transformador puede venir impuesta por un imperativo de funcionamiento en paralelo con otro existente, o bien, como hemos visto, por la necesidad de limitar la corriente de cortocircuito secundaria para salvaguardar la aparamenta existente.
Veamos de forma rápida la incidencia de la tensión de cortocircuito sobre el dimensionamiento del transformador. Asimilaremos Ucc a la reactancia LwI1.
En el corte de la figura, observamos:
Σ1 = Espesor de bobina de BT.
Σ2 = espesor de bobina de AT.
α = distancia entre bobinas de BT y AT.
H = altura de los bobinados.
θm = diámetro de la espira media.
N1 = numero de espiras de AT.
U1 = tensión asignada en AT.
I1 = corriente asignada en AT.
La formula de la reactancia LwI1 % es:
pudiendo simplificar reemplazando todos los valores constantes por k:
Se deduce que:
- El factor preponderante es el cuadrado del numero de espiras.
- El valor de LwI1 es inversamente proporcional a la altura H y proporcional a θm cuyas variaciones son escasas.
Para un volumen de cobre constante, con aumentos de H se reduce LwI1 , Σ1 , Σ2 y θm y acentúan ligeramente el fenómeno.
En el caso inverso se puede aumentar LwI1 por la reducción de H y el aumento de Σ1 , Σ2 y θm
La cota α, que ocupa un importante espacio en el transformador, tiene una influencia notoria y permite ajustar el valor de Ucc incluso cuando otros parámetros hayan sido elegidos.
Aplicación: Se ha visto la influencia del numero de espiras N1.
Los voltios por espira V vienen dados por la formula de Boucherot:
con B = inducción y Sf = sección del núcleo.
B y U1 son valores constantes (B va ligado a la calidad de la chapa, U1 viene impuesta) se observa que N1 es inversamente proporcional a la sección del hierro del núcleo.
Consecuencia practica :
Si las variaciones de Ucc son razonables y si la altura H es sensiblemente constante:
- Para aumentar Ucc habrá que aumentar N1 por consiguiente se reducirá Sf. El volumen de hierro Pv será por tanto menor. Las pérdidas en el hierro Pv serán reducidas, las pérdidas debidas a la carga Pc aumentaran.
- Para reducir Ucc habrá que reducir N1 por consiguiente aumentara Sf y el volumen de hierro. Las pérdidas en el hierro Pv aumentaran, las pérdidas debidas a la carga Pc disminuyen. El dimensionamiento general del transformador aumenta.
En resumen:
FUENTES BIBLIOGRÁFICAS:
Alsthom: Transformadores y Redes
Enrique Ras Oliva: Transformadores de Potencia, de Medida y de Protección
POST EN PDF EN LA SIGUIENTE URL:
http://www.mediafire.com/download/ybhc2zvq8umixcn/Influencia_de_la_tensi%C3%B3n_de_cortocircuito.pdf
POSTS RELACIONADOS:
Intensidad de cortocircuito en un transformador de tres arrollamientos
http://imseingenieria.blogspot.com.es/2016/02/medida-de-la-tension-de-cortocircuito-y.html













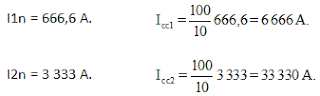








No hay comentarios:
Publicar un comentario