Calentamiento
En las
barras, al igual que en la mayoría de los elementos eléctricos, hay que
considerar dos tipos de calentamiento:
● El
producido por la corriente de empleo que, en condiciones normales de
funcionamiento, es una corriente permanente o de larga duración. Este
calentamiento suele venir limitado por la permisividad de los elementos
próximos a las barras y, en general, para una temperatura ambiente de 30º C,
suele estar alrededor de los 60 K. Ello da una temperatura de 90º C, no
obstante es de advertir que este valor puede ser sobrepasado p. e. si lo
permiten los materiales circundantes, o bien puede quedar a un nivel inferior
si p. e. la carga es inferior a la que permite la sección de la barra.
● El
producido en condiciones anormales o de fallo, siendo el caso extremo el de una
corriente de cortocircuito. En este caso, la corriente es de corta duración;
menor de 5 segundos, siendo fijada por el tiempo de disparo de las
protecciones. La temperatura máxima alcanzable viene dada por:
o
La
permisividad momentánea del material envolvente, en el caso de barras
encapsuladas o protegidas por una envolvente. En cada caso particular el
fabricante debe estar en disposición de proporcionar información al respecto.
o
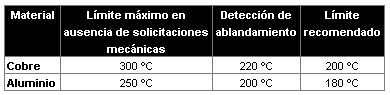
Las
características físicas de la propia barra, en el caso de barras desnudas. Tanto
el Cu como el Al presentan un límite tolerable en casos de ausencia de
solicitaciones mecánicas, pero que no es aconsejable de un modo general porque,
antes de llegar a este límite, el material sufre un cierto ablandamiento que
puede afectar a las uniones y derivaciones.
De ahí que lo recomendable sea quedarse por debajo de este límite de
ablandamiento.
Valor I2t
Al considerar las puntas de calentamiento
producidas por sobreintensidades de corta duración (menos de 5 segundos) se
supone que el calentamiento es adiabático, es decir, se supone que toda la
energía manifestada en el interior de la barra se invierte en aumentar la
temperatura de la barra, y se desprecia el calor evacuado al exterior en el
corto tiempo considerado.
Si la barra tiene una resistencia R y la
sobreintensidad considerada es de un valor eficaz I, la energía w manifestada
en el tiempo t vale:
W = R · I2 ·
t
El producto I2 t, es un índice de la
energía manifestada. Cuando hablamos del I2 t de una barra nos
referimos a la energía que es capaz de absorber la barra sin que su punta de
temperatura momentánea no rebase el límite permitido o recomendado.
El valor I2t se expresa en A2
s. Si hablamos p. e. de un I2 t = 40000 A2 s igual nos
podemos referir a 100 A durante 4 segundos que a 200 A durante 1 segundo.
El valor I2t se da tanto en función
de la temperatura máxima alcanzable como de la temperatura inicial de partida.
No es lo mismo que el proceso se inicie estando la barra fría (a temperatura
ambiente) que estando ya caliente a temperatura de régimen.
Valor I2t
frente al cortocircuito: Cálculos
El valor I2 t es un índice de la
energía que es capaz de acumular una barra o pletina en un tiempo corto, no
superior a 5 segundos, al ser recorrida por una fuerte punta de corriente, p.
e. en caso de cortocircuito, de manera que la punta de calentamiento resultante
sea aún tolerable.
Se supone que la situación evoluciona de forma
adiabática.
Supongamos una barra recorrida por una
corriente I, y en un momento t0 se produce un fuerte incremento que se extingue
en el instante t.
La energía W puesta en juego en el interior de
la barra en el tiempo t = tf - t0 valdrá:
Siendo:
I: valor eficaz de la corriente I en el período
t, en A.
l: longitud de la barra, en m.
R: resistencia de la barra, en Ω.
s: sección de la barra en mm2.
t: tiempo tf - t0, en s
ρ : resistividad de la barra, en Ω · mm2/m.
Si esta energía W la invertimos, toda ella, en
calentar la barra, esta experimenta un aumento de temperatura Δϑ que
vale:
Siendo:
C: calor específico de la barra, en W - s/cm3
· K
V: volumen de la barra, en cm3 (l en
m x S en mm2)
De la combinación de ambas igualdades resulta:
La resistividad ρ a considerar es la que corresponde a la temperatura media durante el período t. Si la temperatura de la barra pasa de un valor inicial ϑ1 a un valor final ϑ2, podemos considerar que la temperatura media sea: ½ ( ϑ 1 + ϑ 2)
Si la resistividad conocida es ρ20 referida a 20º C y la
resistividad a considerar es la que corresponde a la temperatura ϑ tendremos:
La resistividad a considerar es la que corresponde a la
temperatura media durante el período t. Si la temperatura de la barra pasa de
un valor inicial ϑ1 a un valor final ϑ2,
podemos considerar que la temperatura media sea: ½ ( ϑ 1 + ϑ 2)
Si la resistividad conocida es ρ20 referida a 20º C y la
resistividad a considerar es la que corresponde a la temperatura ϑ tendremos:
Siendo δ el factor de temperatura.
El calor específico C podemos considerarlo
constante dentro del campo de temperaturas indicado.
Para el cobre y el aluminio tenemos:
Aplicando estos valores a las fórmulas
anteriores resultan los valores K2 siguientes:
K2 = 14.687 para el Cu; K = 121.1
K2 = 5.286 para el Al; K = 72.70
Suponiendo la misma temperatura final ϑ2
pero considerando temperaturas iniciales distintas obtenemos los siguientes
valores para K2 y K:
Dado que las barras suelen estar a la salida
inmediata de los transformadores los valores de la siguiente tabla pueden
simplificar los cálculos en numerosos casos.
Para el dimensionado de barras, en principio se
determina la sección y con este dato queda también determinado el valor I2
t de la barra. A continuación se verifica que este I2 t sea superior
al resultante de la previsible corriente de cortocircuito y el tiempo de
actuación de las protecciones. Caso contrario habrá que aumentar
consecuentemente la sección de las barras, o disponer protecciones más rápidas,
o adoptar una solución mixta.
Dilatación
Otro efecto térmico de la corriente es el de la
dilatación lineal que experimentan las barras como consecuencia del aumento de
temperatura resultante del paso de la corriente y subsiguientes contracciones
en los períodos de reposo.
Estas variaciones lineales, al ser rígidas las
pletinas pueden traducirse en considerables solicitaciones mecánicas en las
mismas pletinas o en sus soportes. Así p. e. si suponemos una pletina de 10 x
100 mm firmemente anclada en ambos extremos y sujeta a una variación de
temperatura de 50 K, el esfuerzo que ejerce en ambos extremos, es de:
●
7500 Kg si es de aluminio.
●
11050 Kg si es de cobre.
Se ve claramente la necesidad de disponer
dispositivos o juntas de dilatación que permitan el deslizamiento en los
soportes, bornes, puntos de unión, etc.
Dilatación:
Cálculos
Si tenemos una barra rígida de longitud L1
metros y pasa de una temperatura ϑ1, a
otra ϑ2 experimenta una dilatación lineal o variación de longitud ΔL que podemos calcular mediante la fórmula.
Siendo δ el coeficiente de dilatación, que
vale:
●
0,000017 para el cobre.
●
0,000023 para el aluminio.
Si esta barra se encuentra firmemente anclada
en sus extremos de manera que no pueda desplazarse la variación de
longitud ΔL se traduce en una solicitud
mecánica de manera que:
Siendo:
ΔL: Variación
de longitud, en m.
P:
Solicitud mecánica, en kp.
L1:
Longitud de la pletina a la temperatura inicial ϑ1: en m.
E:
Módulo de elasticidad, en kp/mm2: 13.000 para el Cu; 6500 para el
Al.
s:
Sección de la barra o pletina, en mm2.
Comparando las dos fórmulas anteriores podemos
escribir:
Si consideramos
ϑ2 - ϑ1 = 1
K y s = 1 mm2 obtendremos el esfuerzo específico
P = δ · E (kp/k
· mm2) de manera que dada una sección s de barra y una diferencia de
temperatura Δϑ , el esfuerzo mecánico de
tracción o comprensión será:
El valor del esfuerzo específico es:
ρ = 0,221 kp/k.mm2 para el cobre
ρ= 0,15
Kp/k.mm2 para el aluminio
Ejemplo:
Sea una barra de 10 m de longitud y 10 x 100 mm2
de sección que se calienta Δϑ = 50 k.
Posts relacionados:
Barras
conductoras: Efectos electrodinámicos en caso de cortocircuito
Barras
conductoras: Resonancia mecánica, en caso de cortocircuito y en servicio normal
Barras
conductoras: Disposición




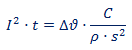










No hay comentarios:
Publicar un comentario