Un gran
número de combinaciones de propiedades y mecanismos de envejecimiento podrían
servir para explicar el modo de deterioro del sistema de aislamiento del que
forman parte los transformadores.
Donde t es el tiempo, y k es la constante de la tasa de reacción de la reacción
química involucrada, sea:
siendo
T la temperatura absoluta.
Cuando las propiedades en estudio lleguen a un valor límite P = Plim, se habrá
alcanzado el final de la vida del transformador. La duración de vida viene en
tal caso definida por:
Montsinger estableció empíricamente una fórmula parecida:
Donde p es una constante y θ es la temperatura en grados Celsius.
Estas expresiones de la duración de vida están asociadas a una propiedad
específica del material asumiendo un valor límite y condiciones experimentales
precisas. La constante de la tasa de reacción es la de la reacción química
básica. Sin embargo, se ha demostrado experimentalmente que las constantes p y
B dependen de las características de aislamiento, lo que significa que el
aumento de temperatura necesario para duplicar la velocidad de envejecimiento
depende también de estas características.
Otra constatación experimental indica que las propiedades mecánicas de los
aislantes se alteran a ritmos diferentes. Por ejemplo, un papel donde el DP (grado de polimerización) se
sitúa entre 200 y 300 puede tener una resistencia a la tracción residual de 40
a 60% pero una resistencia residual a la perforación de 15 a 25%.
La fórmula de Arrenius-Dakin corresponde a los resultados obtenidos en
condiciones experimentales definidas. Sin embargo, la velocidad de la reacción
química que modifica las propiedades mecánicas dependen fuertemente del medio
ambiente de los materiales en reacción. Una concentración en oxígeno y un
contenido en agua más elevados como la presencia de productos favorecerían el
destrucción, aumentando la velocidad de reacción. Las opiniones difieren en
cuanto a la influencia de estos factores sobre la velocidad de descomposición
de la celulosa. Existen informes que indican, para un número dado de escisión
de la molécula de la celulosa, la velocidad de reacción es proporcional al
contenido en agua y esta es aproximadamente tres veces mayor en un medio rico
en oxígeno que en un medio pobre en oxígeno.
Si las condiciones ambientales no son conocidas, la evaluación de la tasa de
reacción puede ser errónea en un factor de tres o cuatro. Si la temperatura del
papel no se mide y solamente es evaluada por medios o métodos imprecisos, por
ejemplo los descritos en las normas existentes, se introduce en tal caso un
error suplementario que eleva la tasa de reacción (y la duración de vida) al
orden del doble.
Las características químicas medioambientales en que se encuentran los
aislantes son difíciles de determinar en todo caso. Las ecuaciones que
determinan la duración de vida con la temperatura son de utilidad muy limitada
para poder evaluar la duración de vida de los aislantes. Por el contrario, esto
no significa que la temperatura no sea importante.
No existen otras fórmulas generalmente aceptadas para describir el deterioro de
un aislante causado por otras circunstancias. Sin embargo, ha habido tentativas
realizadas sobre modelos reducidos para relacionar el envejecimiento térmico
del papel con el número y gravedad de los esfuerzos axiales y de compresión que
conducen a una avería. Estos experimentos mostraron que el número de averías
mecánicas disminuían con niveles elevados de estrés y con envejecimiento
térmico muy avanzado.
Guías de carga y ensayos funcionales de duración de vida en
transformadores
Las guías de carga de los transformadores se muestran
teniendo en cuenta el corto y el largo plazo.
En el corto plazo se tiene en
cuenta el fallo inmediato a temperaturas elevadas debido a la generación de gas
asociada a la temperatura máxima admisible del punto más caliente.
Desde el punto de vista del largo
plazo, las guías describen el envejecimiento de los materiales y el deterioro
de las propiedades mecánicas del papel aislante después de un periodo de
calentamiento prolongado. El escenario sería el siguiente: a corto plazo, el
papel se degrada convirtiéndose muy vulnerable a las solicitaciones mecánicas y,
finalmente, se encuentra en un estado tal que incluso una fuerza mecánica muy
pequeña provocaría el fallo dieléctrico.
Se pueden hacer varias objeciones
a esta teoría. En primer lugar, esta se fundamenta en las propiedades del papel
y supone que el fallo está directamente asociado a las propiedades mecánicas
del papel. Esto a veces puede ser verdad, pero no en todos los casos. Existen
otros modos de fallo y otros mecanismos de envejecimiento, tales como la
contaminación, la penetración de humedad, los cortocircuitos, las
sobretensiones y otras que además afectan también a otros materiales. En
segundo lugar, la rigidez dieléctrica, habitualmente no se reduce de manera
significativa en el papel que presenta un cierto envejecimiento. Por último, incluso
si el deterioro del papel es importante, las capas de papel que envuelven los
conductores están expuestas a temperaturas y concentraciones de oxígeno y
humedad diferentes, por lo que todas las capas no sufrirán el mismo grado de
deterioro. De hecho, las capas del papel menos degradadas pueden afianzar a las
que están más afectadas.
Se considera en los cálculos, que
el envejecimiento y la duración de vida esperada se determina sólo a partir de
la temperatura del punto más caliente del devanado. Las guías ANSI se sirven de
la fórmula de Arrenius-Dakin basadas en la resistencia a la tracción y de un
criterio de fin de vida definido por una reducción del 50% de la resistencia
inicial. En virtud de esta fórmula, la duración de vida normal es de 65 000
horas (7,4 años) para una temperatura del punto más caliente de 110 ºC. La guía
CEI no da valor para la duración de vida esperada, pero indica que una
temperatura de referencia de 98 ºC para el punto más caliente en contacto con
la celulosa deberá permitir una vida “normal”. El aumento de temperatura
entraña la duplicación de la velocidad de deterioro y lo fija en 6 K.
Nuevamente, este valor está basado en una resistencia a la tracción del 50 %
del valor inicial.
Las guías de carga presuponen que
el papel se va a destruir en el punto más caliente. Sin embargo, parece más
lógico que se destruya en el punto más vulnerable, el cual no tiene porque ser
necesariamente el punto más caliente, ya que las tensiones mecánicas que se
ejercen a lo largo de los bobinados varían de un punto a otro.
La resistencia a la tracción ha
sido elegida más o menos arbitrariamente como propiedad “de referencia”. Otras
propiedades decrecen a ritmos diferentes.
El criterio de fin de vida ha
sido igualmente elegido de manera más o menos arbitraria, y la definición de
fin de vida establecido sobre un porcentaje del valor inicial, puede penalizar
a los materiales que posean valores de resistencia inicial elevados, pero que
su velocidad de deterioro sea superior la
media. Por otra parte, por esta razón,
la fórmula de Arrenius-Dakin puede ser muy imprecisa para la
determinación del envejecimiento del material aislante porque no tiene en
cuenta la influencia del oxígeno y la humedad. La combinación de esta inexactitud
y la incertidumbre en cuanto a la temperatura del punto más caliente puede
falsear los resultados del cálculo de la tasa de envejecimiento (y duración de
vida) e introducir un error correspondiente a una diferencia de temperatura de
10 a 20 K.
Con el fin de mejorar la fórmula
de Arrenius-Dakin y aumentar las posibilidades de evaluación del deterioro del
aislamiento, los factores A y B deberían, no ser constantes, sino más bien
funciones del contenido en agua y de la concentración en oxígeno.



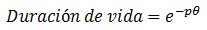
No hay comentarios:
Publicar un comentario